Are you wondering how to apply a decision tree using Python? A Decision Tree is a Supervised Machine Learning algorithm used to categorize or predict outcomes based on the previous dataset. A tree consists of two entities: decision nodes and leaves. Leaves are the outcomes. Decision nodes are where the data is split. In this article, we will discuss decision trees, and implement them in classification and regression problems. Moreover, we will also learn how we can visualize the trained decision trees and evaluate the model.
What is a Decision Tree?
The Decision Tree can solve both classification and regression problems. It is tree-structured, where internal nodes represent the features of a dataset, branches represent the decision rules, and each leaf node represents the decision outcome. The algorithm is called a Decision Tree because, like a tree, it starts with a root node that grows into more branches and forms a tree-like decision structure.
Before going into understanding how the decision tree works and how the training process takes place, we need to understand a few terms that are frequently used in the decision tree.
- Root Node: generally represents the entire sample and gets divided into two or more homogeneous sets. It is the very top node of the decision tree
- Splitting: is a process of dividing a node into two or more sub-nodes
- Decision Node: a node or sub-node that splits data into further sub-nodes
- Leave Node: nodes that do not split is called Leaf or Terminal node; these are the final outputs of the decision tree
- Pruning: the opposite of splitting. When a sub-node of a decision node is removed, the process is called pruning
- Sub-Tree: a subsection of the entire tree is called a branch or sub-tree
- Parent Node: a node, which is divided into sub-nodes is called a parent node
- Child Node: any sub-nodes of a parent node are called Child Node.
Working of Decision tree
For predicting the class of the given dataset, the decision trees algorithm starts from the tree’s root node. It compares the values of the root attribute with the record/dataset attribute and, based on the comparison, follows the branch and jumps to the next node. Then the algorithm compares the attribute value with the other sub-nodes and moves on to the next node. It repeats the process until it reaches the tree’s leaf node. We can summarize the complete process of the decision tree in the following simple steps.
- Let’s say X is the root node that represents the entire dataset. The algorithm will start searching from the root node.
- The algorithm will then find the best attribute in the dataset using any of the Attribute Selection Measure methods.
- The next step is to divide the root node X into subsets that contain possible values for the best attributes.
- Once the subsets are ready, it will generate the decision trees node, which contains the best attribute.
- Recursively create new decision trees using the subsets of the dataset created in the previous step. This step will continue until the nodes can no longer be classified, at that point the final node is referred to as a leaf node.
Decision Tree Using Python for a Regression Problem
A regression dataset is a kind of dataset that contains continuous values as the output or target variable. For this article, we will be using the house pricing dataset. The dataset contains information about houses including the number of rooms, floors, location, and area. You can access the dataset and the Jupyter Notebook for this tutorial from this link. You can download the source code. If you don’t understand any line of code, you can always refer to this blog post. Here we will step by step understand how we can use decision trees for a regression dataset.
Before going to the implementation part, make sure that you have installed the following Python modules, as we will be using them in the implementation part.
- sklearn
- pandas
- NumPy
- matplotlib
- seaborn
You can use the pip command to install these modules on your system.
Exploring the dataset
It is always important to fully understand the dataset that we are going to use to train the model. We will use the pandas module to import and explore the dataset.
# importing the module
import pandas as pd
# importing dataset
dataset = pd.read_csv('house.csv')
# printing rows
dataset.head()Output:
number_of_rooms floor area latitude longitude price
0 1 1 58.0 38.585834 68.793715 330000
1 1 14 68.0 38.522254 68.749918 340000
We have five input variables and price as the output or target variable. As you can see, we have some NULL values as well and as part of preprocessing, we will remove all the null values that exist in the dataset.
# removing null values
dataset.dropna(axis=1, inplace=True)Let us now find, the correlation matrix of the dataset. A correlation matrix is simply a table that displays the correlation coefficients for different variables. The matrix depicts the correlation between all the possible pairs of values in a table. It is a powerful tool to summarize a large dataset and identify and visualize patterns in the given data.
You may like: the ARIMA model in Python
Test and Training Parts
It is highly recommended to split the dataset into testing and training parts so that after training the model, we can use the testing data to evaluate the performance of the model. But before splitting into training and testing datasets, let us first separate the input and output variables.
# dividing into input and output
Input = dataset.drop('price', axis=1)
output = dataset['price']Now, we can split the dataset into testing and training parts. We will use sklearn the splitting function to split the dataset. We will also assign value 1 to the random state.
# splitting the dataaset into Training and Testing Data
from sklearn.model_selection import train_test_split
# test size if 25%
X_train, X_test, y_train, y_test = train_test_split(Input,output,test_size=0.25, random_state=1)As you can see, we have assigned 75% of the data to the training part and 25% to the testing part.
Training the decision tree regressor
Let us now initialize the Decision Tree regressor and train the model on the training dataset. First, we need to import the model from sklearn module.
# importing decision tree using Python
from sklearn.tree import DecisionTreeRegressor
# initializing decision tree using Python model
regressor = DecisionTreeRegressor()The next step is to train the model on the training dataset.
# training decision tree using Python
regressor.fit(X_train,y_train)Once the training is complete, we can move to the predictions and evaluation of the model. But before that, let us visualize the trained decision tree using various methods.
How to visualize a decision tree?
As we know decision trees look like tree structures, where we have a root node, then decision nodes and finally leave nodes. Let us now see, how we can visualize decision trees using Python programming language.
In this section, we will talk about two ways of visualizing decision trees. First, let us visualize the usual decision tree with a root node, decision nodes, and leave nodes.
# importing the plot_tree for decision tree using Python
from sklearn.tree import plot_tree
# output size of decision tree
plt.figure(figsize=(40,20))
# creating a decision tree using Python
plot_tree(regressor, filled=True)
plt.title("Decision tree training for training dataset")
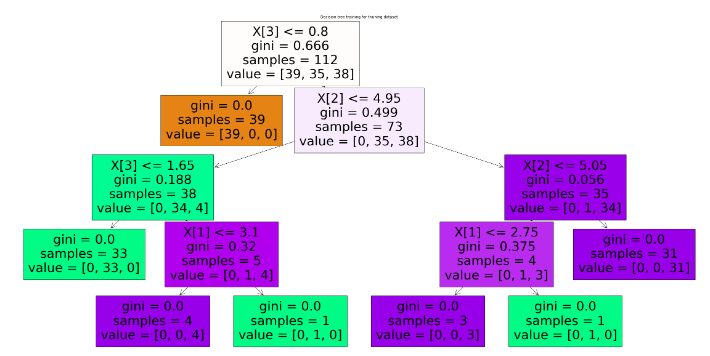
plt.show()The decision tree was so huge and complex that we were not able to take screenshots. Please run the code on your local system and check the tree.
As you can see, we have one root node, then a lot of decision nodes, and then many leaves node.
The second way of visualizing a decision tree is known as text representation. For example, see below:
# importing the tree
from sklearn import tree
# text based tree for decision tree analysis
text_representation = tree.export_text(regressor)
print(text_representation)Output:
|--- feature_2 <= 107.50
| |--- feature_2 <= 61.50
| | |--- feature_0 <= 1.50
| | | |--- feature_4 <= 68.79
| | | | |--- feature_2 <= 41.50
| | | | | |--- feature_1 <= 10.50
| | | | | | |--- feature_2 <= 23.00
| | | | | | | |--- feature_3 <= 38.55
| | | | | | | | |--- feature_2 <= 19.50
| | | | | | | | | |--- value: [30000.00]
| | | | | | | | |--- feature_2 > 19.50
| | | | | | | | | |--- value: [80000.00]
| | | | | | | |--- feature_3 > 38.55
| | | | | | | | |--- value: [136000.00]
| | | | | | |--- feature_2 > 23.00
| | | | | | | |--- feature_3 <= 38.52
| | | | | | | | |--- feature_4 <= 68.73
| | | | | | | | | |--- value: [320000.00]
| | | | | | | | |--- feature_4 > 68.73
| | | | | | | | | |--- feature_4 <= 68.76
| | | | | | | | | | |--- feature_1 <= 6.50
| | | | | | | | | | | |--- truncated branch of depth 9
| | | | | | | | | | |--- feature_1 > 6.50
| | | | | | | | | | | |--- truncated branch of depth 4
| | | | | | | | | |--- feature_4 > 68.76
| | | | | | | | | | |--- feature_2 <= 36.50
| | | | | | | | | | | |--- value: [165000.00]
| | | | | | | | | | |--- feature_2 > 36.50
| | | | | | | | | | | |--- truncated branch of depth 2
| | | | | | | |--- feature_3 > 38.52
| | | | | | | | |--- feature_3 <= 38.53
| | | | | | | | | |--- feature_4 <= 68.75
| | | | | | | | | | |--- feature_1 <= 3.50
| | | | | | | | | | | |--- truncated branch of depth 5
| | | | | | | | | | |--- feature_1 > 3.50
| | | | | | | | | | | |--- truncated branch of depth 2
| | | | | | | | | |--- feature_4 > 68.75
| | | | | | | | | | |--- feature_2 <= 35.00
| | | | | | | | | | | |--- truncated branch of depth 2
| | | | | | | | | | |--- feature_2 > 35.00
| | | | | | | | | | | |--- truncated branch of depth 2
| | | | | | | | |--- feature_3 > 38.53
| | | | | | | | | |--- feature_1 <= 5.50
| | | | | | | | | | |--- feature_3 <= 38.53
| | | | | | | | | | | |--- truncated branch of depth 9
| | | | | | | | | | |--- feature_3 > 38.53
| | | | | | | | | | | |--- truncated branch of depth 10
| | | | | | | | | |--- feature_1 > 5.50
| | | | | | | | | | |--- feature_3 <= 38.59
| | | | | | | | | | | |--- truncated branch of depth 7
| | | | | | | | | | |--- feature_3 > 38.59
| | | | | | | | | | | |--- value: [390000.00]
| | | | | |--- feature_1 > 10.50
| | | | | | |--- feature_4 <= 68.77
| | | | | | | |--- feature_1 <= 12.50
| | | | | | | | |--- feature_2 <= 39.00
| | | | | | | | | |--- feature_2 <= 35.00
| | | | | | | | | | |--- feature_1 <= 11.50
| | | | | | | | | | | |--- value: [131670.00]
| | | | | | | | | | |--- feature_1 > 11.50
| | | | | | | | | | | |--- value: [131092.00]
| | | | | | | | | |--- feature_2 > 35.00
| | | | | | | | | | |--- value: [146982.50]
| | | | | | | | |--- feature_2 > 39.00
| | | | | | | | | |--- feature_1 <= 11.50
| | | | | | | | | | |--- feature_4 <= 68.74
| | | | | | | | | | | |--- value: [163590.00]
| | | | | | | | | | |--- feature_4 > 68.74
| | | | | | | | | | | |--- value: [163600.00]
| | | | | | | | | |--- feature_1 > 11.50
| | | | | | | | | | |--- value: [162872.00]
| | | | | | | |--- feature_1 > 12.50
| | | | | | | | |--- feature_3 <= 38.57
| | | | | | | | | |--- feature_4 <= 68.75
| | | | | | | | | | |--- feature_2 <= 35.00
| | | | | | | | | | | |--- truncated branch of depth 3
| | | | | | | | | | |--- feature_2 > 35.00
| | | | | | | | | | | |--- truncated branch of depth 2
| | | | | | | | | |--- feature_4 > 68.75
| | | | | | | | | | |--- value: [115000.00]
| | | | | | | | |--- feature_3 > 38.57
| | | | | | | | | |--- feature_1 <= 16.50
| | | | | | | | | | |--- feature_2 <= 40.50
| | | | | | | | | | | |--- truncated branch of depth 3
| | | | | | | | | | |--- feature_2 > 40.50
| | | | | | | | | | | |--- value: [150000.00]
| | | | | | | | | |--- feature_1 > 16.50
| | | | | | | | | | |--- feature_1 <= 17.50
| | | | | | | | | | | |--- value: [115963.00]
| | | | | | | | | | |--- feature_1 > 17.50
| | | | | | | | | | | |--- value: [120000.00]
| | | | | | |--- feature_4 > 68.77
| | | | | | | |--- value: [235000.00]
| | | | |--- feature_2 > 41.50
| | | | | |--- feature_1 <= 9.50
| | | | | | |--- feature_4 <= 68.77
| | | | | | | |--- feature_4 <= 68.74
| | | | | | | | |--- feature_3 <= 38.51
| | | | | | | | | |--- feature_2 <= 47.00
| | | | | | | | | | |--- value: [350000.00]
| | | | | | | | | |--- feature_2 > 47.00
| | | | | | | | | | |--- feature_3 <= 38.50
| | | | | | | | | | | |--- value: [399000.00]
| | | | | | | | | | |--- feature_3 > 38.50
| | | | | | | | | | | |--- truncated branch of depth 2
| | | | | | | | |--- feature_3 > 38.51
| | | | | | | | | |--- feature_3 <= 38.59
| | | | | | | | | | |--- feature_3 <= 38.55
| | | | | | | | | | | |--- truncated branch of depth 7
| | | | | | | | | | |--- feature_3 > 38.55
| | | | | | | | | | | |--- truncated branch of depth 13
| | | | | | | | | |--- feature_3 > 38.59
| | | | | | | | | | |--- value: [420000.00]
| | | | | | | |--- feature_4 > 68.74
| | | | | | | | |--- feature_3 <= 38.53
| | | | | | | | | |--- feature_2 <= 48.00
| | | | | | | | | | |--- value: [430000.00]
| | | | | | | | | |--- feature_2 > 48.00
| | | | | | | | | | |--- feature_4 <= 68.75
| | | | | | | | | | | |--- value: [456000.00]
| | | | | | | | | | |--- feature_4 > 68.75
| | | | | | | | | | | |--- value: [455000.00]
| | | | | | | | |--- feature_3 > 38.53
| | | | | | | | | |--- feature_4 <= 68.75
| | | | | | | | | | |--- feature_1 <= 5.00
| | | | | | | | | | | |--- truncated branch of depth 3
| | | | | | | | | | |--- feature_1 > 5.00
| | | | | | | | | | | |--- value: [423000.00]
| | | | | | | | | |--- feature_4 > 68.75
| | | | | | | | | | |--- feature_3 <= 38.56
| | | | | | | | | | | |--- truncated branch of depth 5
| | | | | | | | | | |--- feature_3 > 38.56
| | | | | | | | | | | |--- truncated branch of depth 6
| | | | | | |--- feature_4 > 68.77
| | | | | | | |--- feature_3 <= 38.60
| | | | | | | | |--- feature_2 <= 57.00
| | | | | | | | | |--- feature_4 <= 68.78
| | | | | | | | | | |--- feature_3 <= 38.54
| | | | | | | | | | | |--- truncated branch of depth 11
| | | | | | | | | | |--- feature_3 > 38.54
| | | | | | | | | | | |--- value: [390000.00]
| | | | | | | | | |--- feature_4 > 68.78
| | | | | | | | | | |--- feature_2 <= 47.50
| | | | | | | | | | | |--- value: [240000.00]
| | | | | | | | | | |--- feature_2 > 47.50
| | | | | | | | | | | |--- value: [110000.00]
| | | | | | | | |--- feature_2 > 57.00
| | | | | | | | | |--- feature_1 <= 8.50
| | | | | | | | | | |--- value: [300000.00]
| | | | | | | | | |--- feature_1 > 8.50
| | | | | | | | | | |--- value: [325000.00]
| | | | | | | |--- feature_3 > 38.60
| | | | | | | | |--- feature_1 <= 4.50
| | | | | | | | | |--- value: [430000.00]
| | | | | | | | |--- feature_1 > 4.50
| | | | | | | | | |--- value: [234000.00]
| | | | | |--- feature_1 > 9.50
| | | | | | |--- feature_2 <= 42.50
| | | | | | | |--- feature_4 <= 68.77
| | | | | | | | |--- feature_1 <= 12.50
| | | | | | | | | |--- value: [380000.00]
| | | | | | | | |--- feature_1 > 12.50
| | | | | | | | | |--- value: [400000.00]
| | | | | | | |--- feature_4 > 68.77
| | | | | | | | |--- value: [450000.00]
| | | | | | |--- feature_2 > 42.50
| | | | | | | |--- feature_3 <= 38.59
| | | | | | | | |--- feature_4 <= 68.74
| | | | | | | | | |--- feature_4 <= 68.72
| | | | | | | | | | |--- feature_3 <= 38.56
| | | | | | | | | | | |--- truncated branch of depth 3
| | | | | | | | | | |--- feature_3 > 38.56
| | | | | | | | | | | |--- truncated branch of depth 3
| | | | | | | | | |--- feature_4 > 68.72
| | | | | | | | | | |--- feature_1 <= 15.00
| | | | | | | | | | | |--- truncated branch of depth 9
| | | | | | | | | | |--- feature_1 > 15.00
| | | | | | | | | | | |--- truncated branch of depth 4
| | | | | | | | |--- feature_4 > 68.74
| | | | | | | | | |--- feature_3 <= 38.51
| | | | | | | | | | |--- feature_2 <= 55.00
| | | | | | | | | | | |--- truncated branch of depth 2
| | | | | | | | | | |--- feature_2 > 55.00
| | | | | | | | | | | |--- value: [17000.00]
| | | | | | | | | |--- feature_3 > 38.51
| | | | | | | | | | |--- feature_3 <= 38.55
| | | | | | | | | | | |--- truncated branch of depth 9
| | | | | | | | | | |--- feature_3 > 38.55
| | | | | | | | | | | |--- truncated branch of depth 6
| | | | | | | |--- feature_3 > 38.59
| | | | | | | | |--- value: [450000.00]
| | | |--- feature_4 > 68.79
| | | | |--- feature_2 <= 45.50
| | | | | |--- feature_2 <= 27.00
| | | | | | |--- feature_1 <= 5.00
| | | | | | | |--- feature_1 <= 1.50
| | | | | | | | |--- feature_2 <= 25.50
| | | | | | | | | |--- value: [200000.00]
| | | | | | | | |--- feature_2 > 25.50
| | | | | | | | | |--- value: [129000.00]
| | | | | | | |--- feature_1 > 1.50
| | | | | | | | |--- feature_2 <= 24.50
| | | | | | | | | |--- feature_4 <= 68.81
| | | | | | | | | | |--- value: [220000.00]
| | | | | | | | | |--- feature_4 > 68.81
| | | | | | | | | | |--- feature_1 <= 3.00
| | | | | | | | | | | |--- value: [245000.00]
| | | | | | | | | | |--- feature_1 > 3.00
| | | | | | | | | | | |--- value: [240000.00]
| | | | | | | | |--- feature_2 > 24.50
| | | | | | | | | |--- feature_2 <= 25.50
| | | | | | | | | | |--- value: [300000.00]
| | | | | | | | | |--- feature_2 > 25.50
| | | | | | | | | | |--- feature_1 <= 3.00
| | | | | | | | | | | |--- value: [260000.00]
| | | | | | | | | | |--- feature_1 > 3.00
| | | | | | | | | | | |--- value: [246666.67]
| | | | | | |--- feature_1 > 5.00
| | | | | | | |--- value: [110000.00]
| | | | | |--- feature_2 > 27.00
| | | | | | |--- feature_1 <= 4.50
| | | | | | | |--- feature_2 <= 37.50
| | | | | | | | |--- feature_2 <= 36.00
| | | | | | | | | |--- feature_2 <= 29.50
| | | | | | | | | | |--- feature_1 <= 3.00
| | | | | | | | | | | |--- value: [353000.00]
| | | | | | | | | | |--- feature_1 > 3.00
| | | | | | | | | | | |--- truncated branch of depth 2
| | | | | | | | | |--- feature_2 > 29.50
| | | | | | | | | | |--- feature_2 <= 32.50
| | | | | | | | | | | |--- truncated branch of depth 4
| | | | | | | | | | |--- feature_2 > 32.50
| | | | | | | | | | | |--- truncated branch of depth 4
| | | | | | | | |--- feature_2 > 36.00
| | | | | | | | | |--- value: [452000.00]
| | | | | | | |--- feature_2 > 37.50
| | | | | | | | |--- feature_3 <= 38.55
| | | | | | | | | |--- feature_1 <= 3.50
| | | | | | | | | | |--- feature_2 <= 44.50
| | | | | | | | | | | |--- truncated branch of depth 4
| | | | | | | | | | |--- feature_2 > 44.50
| | | | | | | | | | | |--- value: [400000.00]
| | | | | | | | | |--- feature_1 > 3.50
| | | | | | | | | | |--- value: [186800.00]
| | | | | | | | |--- feature_3 > 38.55
| | | | | | | | | |--- feature_4 <= 68.80
| | | | | | | | | | |--- feature_1 <= 2.50
| | | | | | | | | | | |--- truncated branch of depth 3
| | | | | | | | | | |--- feature_1 > 2.50
| | | | | | | | | | | |--- truncated branch of depth 5
| | | | | | | | | |--- feature_4 > 68.80
| | | | | | | | | | |--- value: [2000.00]You can use any of the above methods to visualize the decision tree.
Testing Decision tree regressor
Now, we will use input data to make predictions using the trained decision tree model. As we know, the input variables were the number of rooms, floor, area, and location. So, we will use some random data and use the model to predict the price of the house.
# making predictions
regressor.predict([[2, 2, 57, 38.8, 68.6]])Output:
array([700000])
As you can see, the model has predicted the price of the house. But the problem is that we don’t know how accurate this prediction is. So, to see how well our model is predicting, we will use the testing data to make predictions and will compare those predictions with actual values.
# making predictions / decision tree using Python
y_pred = regressor.predict(X_test)Now, we will move to evaluate the performance of the model.
Evaluating the decision tree regressor
First, let us visualize the actual and the predicted values so that we will have an idea of how close our predictions are to the actual values.
# importing the module
import matplotlib.pyplot as plt
# fitting the size of the plot
plt.figure(figsize=(20, 8))
# plotting the graphs
plt.plot([i for i in range(len(y_test))],y_pred, label="Predicted values")
plt.plot([i for i in range(len(y_test))],y_test, label="actual values")
plt.legend()
plt.show()Output:
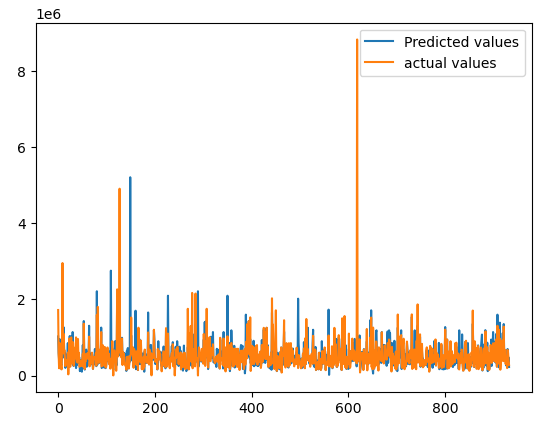
As you can see, the plot shows that the model was able to follow the trend and the predictions are pretty much close to the actual values.
Now, we will use the R-square score to see how close the predictions are to the actual values R-square score is usually between 1 and 0. The closer the value is to zero, the better the predictions are.
# Importing r2
from sklearn.metrics import r2_score
# Evaluating the model
print('R-square score is :', r2_score(y_pred, y_test))Output:
The R-square score is: 0.1199975
The R-square suggests that the model was able to follow the trend and hidden patterns.
Decision trees using Python for a classification problem
As we have already implemented how we can use decision trees to solve regression problems, now we will jump to solve classification problems using a decision tree classifier. A classification problem/dataset is a dataset having categorical values in the output class. Here, we will be using the very famous classification dataset iris. You can access the source code from GitHub and refer to this article wherever ever explanation is needed.
Importing and exploring the dataset
We need to import the sklearn module and load the iris dataset from there.
# importing dataset
from sklearn import datasets
# importing the dataset
iris = datasets.load_iris()Once the dataset is loaded, we will then convert the dataset into pandas Dataframe along with headings.
# importing required modules
import pandas as pd
import numpy as np
# converting to pandas dataframe
dataset = pd.DataFrame(data= np.c_[iris['data'], iris['target']],
columns= iris['feature_names'] + ['target'])
# heading of the dataset
dataset.head()The dataset contains information about three different types of flowers. We can visualize the distribution of each of the input attributes using a violin plot.
Splitting the dataset for train and test parts
Now, we will move to the splitting part. Here we will split the dataset into testing and training parts so that we can use the training dataset to train the model and the testing dataset to evaluate the performance of the model.
First, let us split the dataset into input and output variables.
# splitting the dataset
X= dataset.drop('target', axis=1)
y = dataset['target']Now we will divide the dataset into testing and training parts.
# splitting the dataaset into Training and Testing Data
from sklearn.model_selection import train_test_split
# test size if 25%
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.25)As you can see, we have assigned 25% of the dataset to the testing part and the remaining 75% to the training part.
Training and testing the decision tree classifier
Now, let us import the decision tree classifier and train the model on the training dataset, and then use the testing dataset to evaluate the model.
# importing decision tree using Python
from sklearn.tree import DecisionTreeClassifier
# inializing decision tree using Python
classifer = DecisionTreeClassifier()
# providing the training dataset
classifer.fit(X_train,y_train)Once the training is complete, we can then use the testing data to make predictions.
# making predictions
y_pred =classifer.predict(X_test)Visualizing and creating a decision tree classifier
Now, we will use the plot_tree module to visualize the decision tree classifier.
# importing the plot tree method
from sklearn.tree import DecisionTreeClassifier, plot_tree
# output size of decision tree using Python
plt.figure(figsize=(40,20))
# plotting the decision tree using Python
plot_tree(classifer, filled=True)
plt.title("Decision tree training for training dataset")
plt.show()Output:
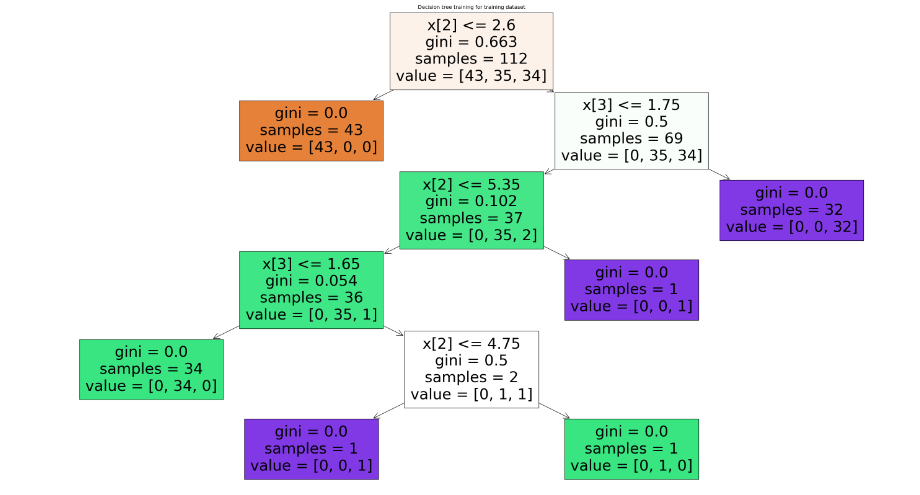
Now let us use different evaluation matrices to evaluate the decision tree classifier.
Evaluation of decision tree classifier
Let us first plot the confusion matrix of the decision tree classifier. The confusion matrix is a matrix used to determine the performance of the classification models for a given set of test data. It can only be determined if the true values for test data are known.
# creating confusion matrix for decision trees using Python
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test,y_pred)
# Making the Confusion Matrixfor decision trees using Python
cm = confusion_matrix(y_pred, y_test)
sns.heatmap(cm,annot=True)Output:
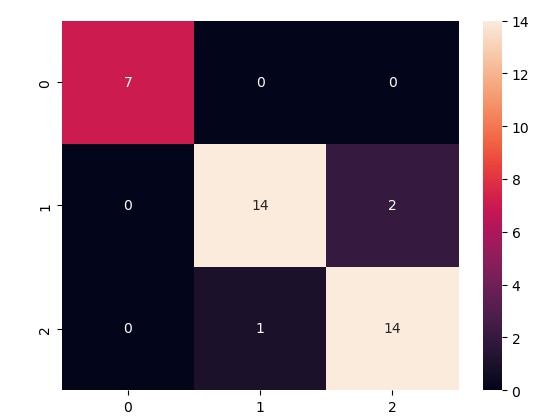
The simplest way to understand the confusion matrix is all the values in the main diagonal show correctly classified and everything outside the main diagonal is incorrectly classified.
Let us now also find the accuracy score of the model.
# importing the required module and methods
from sklearn.metrics import accuracy_score
print(f'Accuracy-score: {accuracy_score(y_test, y_pred):.3f}')Output:
Accuracy-score: 0.974
This shows that the model was able to classify 97% of the testing data correctly.
Summary
Decision trees use multiple algorithms to decide to split a node into two or more sub-nodes. The creation of sub-nodes increases the homogeneity of resultant sub-nodes. In this article, we learned about decision trees and implemented decision trees on regression and classification datasets. We also visualized the decision trees and used various evaluation matrices to evaluate the decision tree models.